Progress report - prime path coverage in gcc

After the success of getting MC/DC support into gcc, NASA decided to keep funding the project and focus on (prime) path coverage. I have been working on this problem for a while now and it is about time to write a post on the progress so far.

Prime paths

The number of paths in a program grows very fast. Somewhat simplified, a path is a sequence of blocks evaluated for a run. Any control flow structure – if, for, while, switch, etc. – will multiply the number of paths up until that point. Additionally, loops are problematic because taking the loop zero times, one time, two times etc. are all different paths.

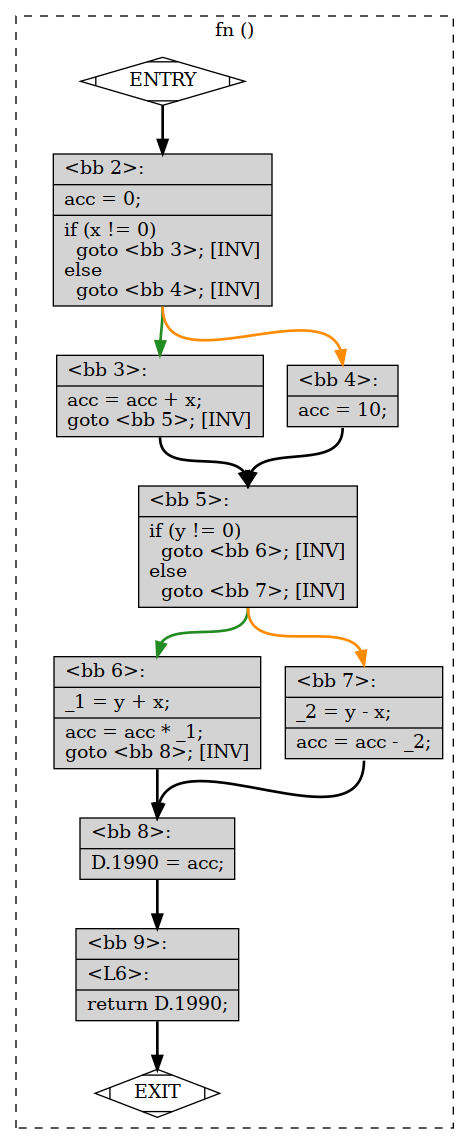
Let’s take a step back and look at a real program. This program has no loops, and the paths from entry to exit are not too surprising. The entry and exit vertices are omitted.

2 3 5 6 8
2 3 5 7 8
2 4 5 6 8
2 4 5 7 8

int fn (int x, int y) {
    int acc = 0;
    if (x)
        acc += x;
    else
        acc = 10;

    if (y)
        acc *= y + x;
    else
        acc -= (y - x);
    return acc;
}

To address loops we can limit the paths we consider to simple paths. A simple path is a path with no repeated vertices unless the last vertex is also the first vertex, that is, we close a loop. Considering only simple paths eliminates the problem of sequences like [2 4 5 6] [2 4 5 6 4 5 6] [2 4 5 6 2 4 5 6 2 4 5 6] ... which is nice, but they are still problematic. Going back to the fn which has 4 paths between entry and exit – simple paths can start at any vertex, and not just the entry. For the sequence 2 3 5 6 8 we have these simple paths:

2
2 3
2 3 5
2 3 5 6
2 3 5 6 8
3 5
3 5 6
3 5 6 8
5
5 6
5 6 8
6
6 8
8

Note that all of these paths would be covered by a single call where both x and y are non-zero. A prime path is the longest simple path which is not a subpath of any other simple path, and provides a good balance for the number of paths and the quality of coverage. The original 4 paths were all prime paths. That being said, the number of prime paths still grows very fast – this program has 14 prime paths.

while (a) {
    if (b)
        return;
    while (c--)
        a = fn(c);
}

Finding the paths

To find the prime paths of a function we need a good algorithm. A straight forward naïve implementation simply doesn’t finish for even reasonably sized problems. For examplple, I have experimented with tree. The function unix_getfulltree in tree.c has just short of a million paths, and I killed the process after 24 hours.

I found the paper Time and Space-Efficient Compositional Method for Prime and Test Paths Generation by Fazli & Afsharchi which describe a neat algorithm for finding prime paths, and I implemented it in gcc. That algorithm, combined with a suffix tree, brings the runtime down to something managable. I find the approx. two million paths in tree.c in less than four seconds. It is important that finding paths is fast, because the paths are too large to store explicitly, and gcov will have to recompute them.

I am certain my program can still be improved, speed-wise. About half the time is spent adding entries into the suffix tree (which is good), and I think a better algorithm would significantly cut down the search time. At its core there is also a simple recursive function for finding simple paths, which I think could benefit from a more clever algorithm. That being said, you probably won’t bother to try to cover millions of paths, and if path coverage is interesting at all you probably want to refactor anyway. Measuring (and trying to achieve) path coverage effectively forces you into to write programs in a particular style, but this is probably the goal.

Measuring coverage

To measure I applied a technique very similar to the one I used for MC/DC. First, I create a huge bitset where the nth bit corresponds to the nth prime path in the (lexicographically) sorted set of paths. When entering a vertex, a few bitwise operations mask out the bits of paths this vertex is not a part of. Then the paths starting in this vertex are masked in, before finally the paths which end in this vertex are written to the global covered sets. The instrumentation overhead is quite small, but creating so many new nodes in this stage is very punishing for the compiler. For small functions this seems fine, but tree.c takes up to ten minutes or so to build.

The bitset scales with the number of paths, which also means object sizes grow very fast. tree.o ends up being 50M which is just impressive balooning. We might need to come up with something clever to reduce this, but again, you probably want to refactor these types of functions which makes most of the problem go away.

Reporting coverage

So far, I have only sketched out a few alternatives for reporting. The key difference between path coverage and the other coverage reports in gcov is that a path is function wide, and does not have a natural anchor to a single line like statement, branch, and even condition coverage. This also makes line oriented tools like grep less useful.

The solution is probably to report right below the function summaries. I have a few sketches on this, and a few supporting features I will present in a later post. Still, my prototype does simple reporting and I have already found it quite useful to understand what I am measuring.

Going forward

I have posted a message on gcc-patches asking for feedback. There is still a lot of work left to do, but I believe all the key pieces are there. There are a few open questions and a lot of polishing I would like to do over the summer, but I am very hopeful for this feature and I think it will end up being quite useful.